Stress analysis and crack lengths
CADAM3D is based on the gravity method and beam theory for the calculation of stresses along a cracked plane (Figure 194A). The shear stresses are calculated assuming a parabolic distribution for non-cracked sections (USBR 1976). For cracked sections (Figure 194B), the shear stress distribution on the uncracked ligament is influenced by the stress concentration and will be modified according to a more or less triangular distribution (Lombardi 1988). Shear stresses for a cracked joint are not calculated by CADAM3D. Sliding stability analysis is performed using the resultant of shear stresses acting on the ligament. However, to validate the orientation of the analysis plane, the magnitude and orientation of the principal stresses acting on the ligament should be studied. For this purpose, simplified calculations can be performed by assuming a shear stress distribution that satisfies equilibrium.
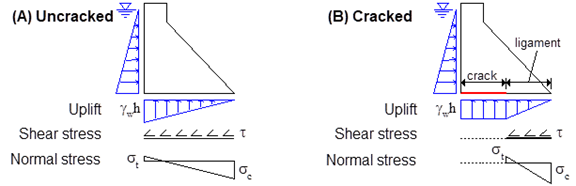
Figure 194 Effect of cracking on uplift pressure and stress distribution
In many cases, when a crack propagates along a joint in contact with the reservoir, the water pressure penetrates the crack producing uplift pressures. Figure 194B shows an example of the increase of the full uplift pressure in a crack. It is obvious that the calculation of crack length is coupled with the increase of uplift pressures in the cracks.
Analytical calculation of crack length: Analytical formulae have been developed to calculate the crack length for simple cases of gravity dams without drains assuming that the tensile strength is zero (Corns et al. 1988a, USBR 1987, FERC 1991). More complex cases considering the presence of drains and tensile strength, using beam theory, have been reported (ANCOLD 1991, Lo et al. 1990 with a linear distribution of normal stresses). However, to consider a range of more complex cases such as inclined joints with different drainage conditions, it is more efficient to calculate the crack length using an iterative method (USBR 1987).
Iterative method to evaluate crack lengths: CADAM3D uses an iterative procedure to calculate the crack length (Figure 195). When the crack initiation criterion indicates the development of a crack, the iterative procedure begins. The crack length is progressively increased, and the uplift pressures are adjusted according to the specified drainage conditions until the crack propagation criterion indicates crack arrest. As mentioned previously two different cracking criteria are available in CADAM3D: initiation and propagation.
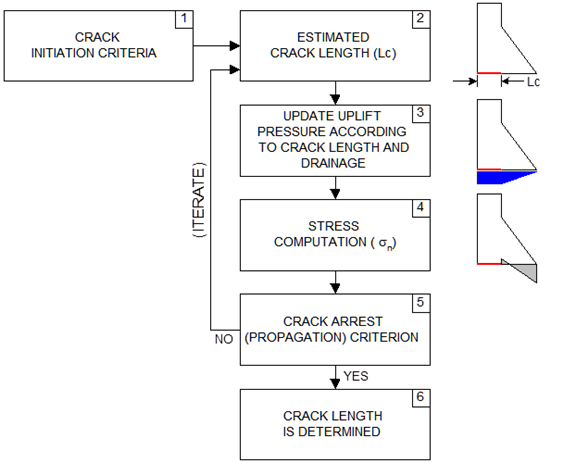
Figure 195 Iterative procedure for calculating crack length
The uplift pressures can be considered as external forces and the stresses at the crack tip, σn, are calculated while including the uplift pressures in the force resultant (USACE 1995, USBR 1987 (crack propagation procedure)). These calculations produce a linear distribution of normal stresses even in cases where a nonlinear distribution of uplift pressures is present due to drainage.
![]()
ΣV = Sum of all vertical forces including uplift pressure
A = Area of uncracked ligament
ΣM = Moment relative to the centroid of the uncracked ligament caused by all loads including uplift pressures.
I = Moment of inertia of uncracked ligament.
c = Distance between the centre of gravity of the uncracked ligament and the position where stresses are calculated.
Initiation (crack propagation) from U/S and D/S faces
When performing static or seismic stress analysis, cracks can be initiated and propagated from either upstream and/or downstream face.
Inclined joints
CADAM3D only considers the upstream-downstream inclination of the plane - the cross- stream inclination is not considered (an average elevation plane can be used in this case).
Figure 196 shows the distribution of uplift pressures along a cracked inclined joint. In this case, the uplift pressures are applied in the direction normal to the crack for stress and stability analysis. Using, in this case, the geometric properties (area, inertia) calculated in a local axis system along the inclined plane.
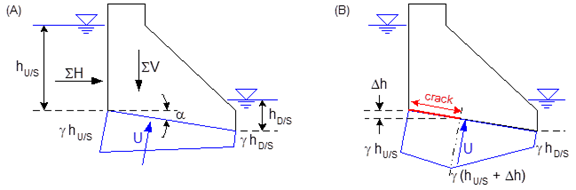
Figure 196 Dam with sloped joint (A): uncracked; (B) cracked