Westergaard Generalized Formulation 3D
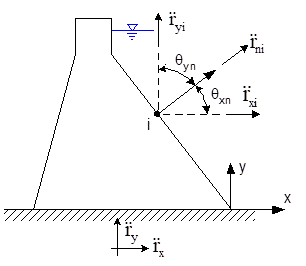
Westergaard's basic formulation for a vertical wall assumes that the acceleration is oriented normal to the wall. However, several concrete dams have been constructed with inclined faces upstream (or downstream). Examples are gravity dams with inclined upstream faces, or arch dams with double curvature, or spillway pier noses. Westergaard's added mass method has been extended to calculate hydrodynamic forces for concrete dams where the orientation of the upstream face with respect to the orientation of the seismic acceleration varies from point to point (Clough 1985, FERC 1999). The pressure Pni acting at any point "i" on the upstream face is given by:
![]()
Hi = Depth of water at point ‘i’
H = Total reservoir depth
yi = Height of point ‘I’
rni = Acceleration normal to point ‘i’
Generalized 2D Westergaard formulation
Generalized 3D Westergaard formulation
In compact notation ![]() represents the pressure per unit of normal acceleration. In 3D the normal acceleration at the upstream face is derived from the cosines between the Cartesian coordinates and the normal (Figure 200, 201).
represents the pressure per unit of normal acceleration. In 3D the normal acceleration at the upstream face is derived from the cosines between the Cartesian coordinates and the normal (Figure 200, 201).
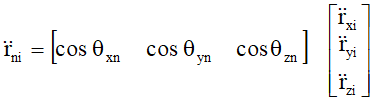
Where:
![]()
The normal pressure function, Pni, is converted into a corresponding normal force function, Fni, by multiplication with the tributary area, Ai.
![]()
Finally, the normal force Fni is transformed into Cartesian coordinates to calculate the horizontal cross-stream and the vertical forces acting on the upstream face. In CADAM 3D we only consider the upstream-downstream stability. The cross-stream and vertical stability are not considered.
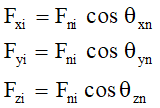
where
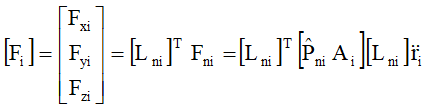
It can be seen that these point forces are equivalent to inertia forces, acting in opposition to the accelerations at point 'i'. The added mass can, therefore, be defined as follows:
![]()
The hydrodynamic effects of the reservoir are then expressed as masses acting at point 'i'
![]()
The [May] matrix is a full 3 x 3 matrix for each point 'i'. There is no rational basis for assuming that the Westergaard parabolic hydrodynamic pressure distribution for a rigid dam with a vertical face applies to a wall with arbitrary geometry. However, the above formulation is fairly accurate when there are no large lateral variations in hydrodynamic pressures along the wall.