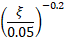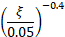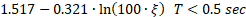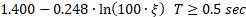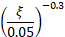Pseudo-dynamic method: Chopra’s method (1988)
Basic assumptions – dynamic amplification
The pseudo-dynamic analysis is based on the simplified response spectrum method as described by Chopra (1988, 2020), and Lokke and Chopra (2013). The user should consult these references for a complete description of the input variables. It is conceptually similar to a pseudo-static analysis, except that it accounts for the dynamic amplification of the inertia forces over the height of the dam. However, the oscillatory nature of amplified inertia forces is not considered..
Seismic accelerations
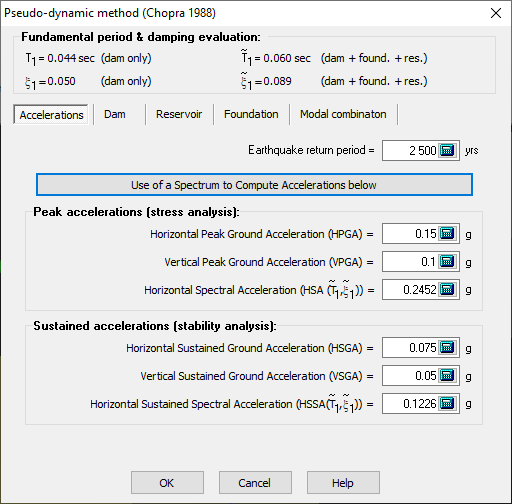
Figure 145
The pseudo-dynamic method does not consider the oscillatory nature of the seismic loads. It is, therefore, appropriate to perform safety assessment in two phases: (a) Maximum stress evaluation using spectral acceleration values, and (b) stability analysis using sustained spectral acceleration values (Figure 145). It is assumed that the dynamic analyses consider only the horizontal acceleration. As the vibration period of the dam in the vertical direction is considered small, it is reasonable to neglect the vertical seismic amplification over the height of the dam.
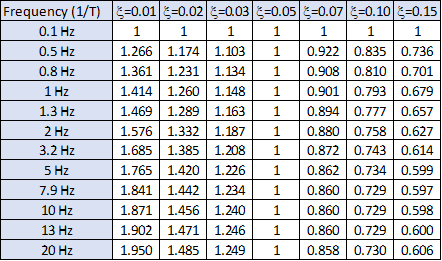
Most acceleration spectra are defined with a damping ratio of 5%. This damping ratio would likely be different when considering the combined dam-foundation-reservoir system. A tool in CADAM3D is available to evaluate the adjusted spectrum corresponding to a damping ratio different from 5% by clicking Use of a Response Spectrum to Calculate accelerations below (Figure 145) which opens the window in Figure 146. The first step is to define the 5% damping spectrum by using Define your spectrum tool.
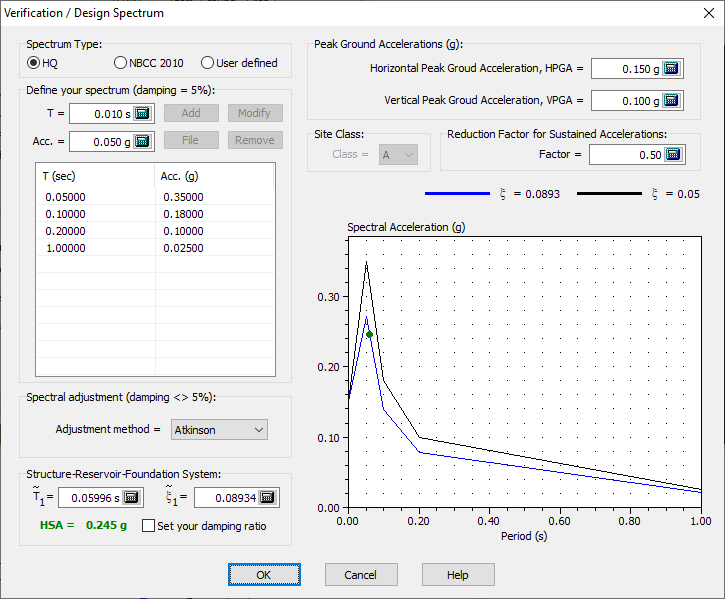
Figure 146
CADAM3D will then calculate the revised spectrum using the modified damping ratio computed for the dam-foundation-reservoir system (blue graph). This value is typed in green in Figure 146. The user can specify a specific damping ratio, different from CADAM3D, by clicking Modify damping.
It should be noted that the Spectral adjustment drop-down list allows the user to choose between seven different methods to adjust spectra according to various damping ratios.
|
Adjustment method |
Adjustment factor |
|
Atkinson and Pierre (2004) |
|
|
AASHTO Koval-WNA* |
|
|
Chile CSA.S6-14 |
|
|
Eurocode 8 |
|
|
(Newmark-Hall) |
|
|
Koval–ENA* |
|
* WNA=Western North America; ENA=Eastern North America
The other types of response spectra that can be used are HQ (Newmark Hall) and NBCC 2010 (only available in a special proprietary version of CADAM3D).
Dam properties
To ensure the accuracy of Chopra's pseudo-dynamic method, the structure must be divided into layers to perform numerical integration. The user can specify the number of divisions, ranging from 11 to 301. The dynamic flexibility of the dam is modeled with the dynamic elastic modulus of concrete (Es). The damping ratio of the dam resting on a rigid foundation without reservoir interaction is necessary to calculate the damping ratio of the dam-foundation-reservoir system (![]() ).
).
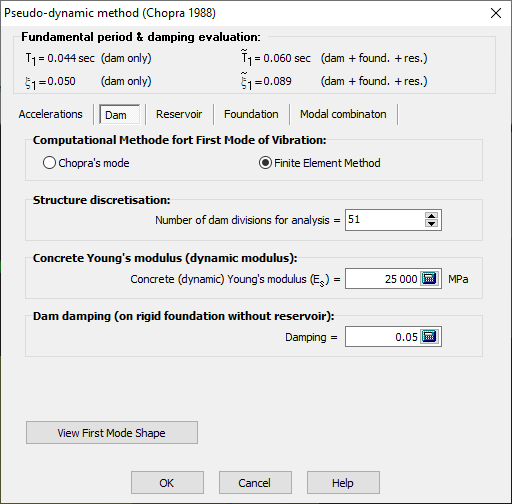
Figure 147
Chopra's pseudo-dynamic method uses a unique normalised fundamental vibration mode based on pre-analyses by finite elements. It should be noted that certain geometric assumptions, were used to establish this fundamental mode. The user should be aware that this method offers excellent results if the geometry, as well as the spatial distribution of the mass of the dam respects Chopra's assumptions. Figure 148 presents the basic normalised vibration mode defined by Chopra. The user can access this window by clicking View First Mode Shape (Figure 147).
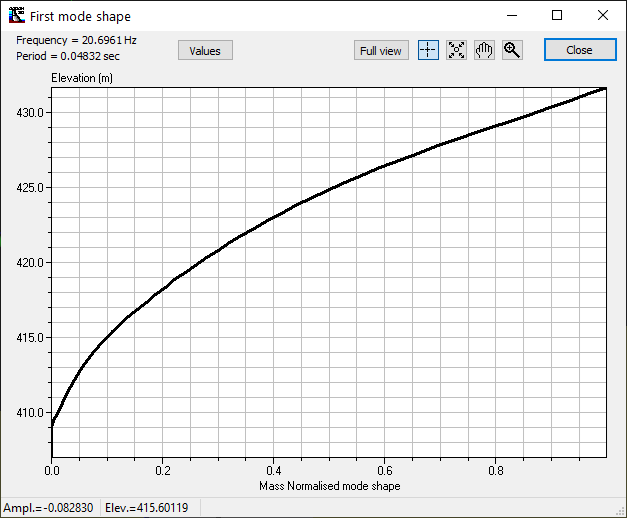
Figure 148
The user can evaluate the first mode based on the geometry of the model using the Finite Element Method (FEM). The option remains the preferred one at all times, especially for structures less than 90m high. Figure 149 presents the normalised vibration mode using FEM. There is a significant difference between the two vibration modes (Chopra Figure 148 vs. FEM Figure 149).
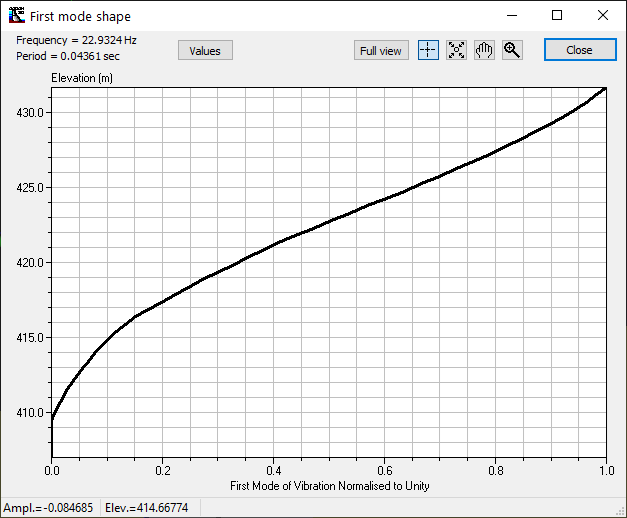
Figure 149
There is a significant difference between the two vibration modes:
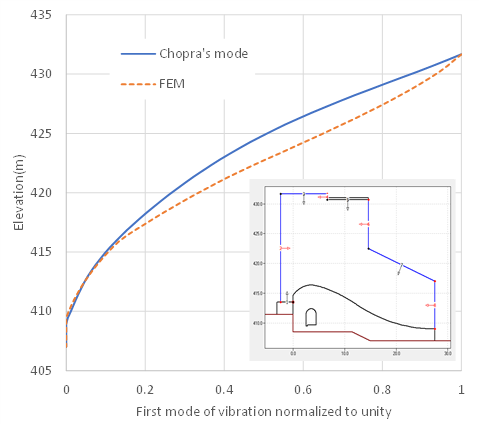
Reservoir properties
The wave reflection coefficient is the ratio of the amplitude of the reflected hydrodynamic pressure wave over the amplitude of a vertical wave pressure at the bottom of the reservoir (Figure 150). A value of = 1 indicates that the pressure waves are fully reflected, while smaller values of indicate higher absorption at the reservoir bottom.
The velocity of pressure waves in water is actually the speed of sound in the water. In general, it is assumed to be at 1440 m/sec (4720 ft/sec).
Figure 150
Foundation properties
The interaction of the dam with the rock foundation changes the fundamental vibration period as well as the damping ratio of the dam-foundation-reservoir system.
The hysteretic damping of the foundation (ηf) has an impact on the damping ratio of the dam-reservoir-foundation system (Figure 151).
Figure 151
The Elevation where the structure is considered embedded refers to the elevation where the structure base is considered fixed, thus the modal displacement will be zero at this elevation and below. This elevation must be located within the minimum and the maximum elevations defined by the foundation profile. This parameter has a significant influence on the structure fundamental mode shape of vibration (see Figure 151). By default, CADAM3D use the average elevation of the upstream and the downstream sides of the foundation.
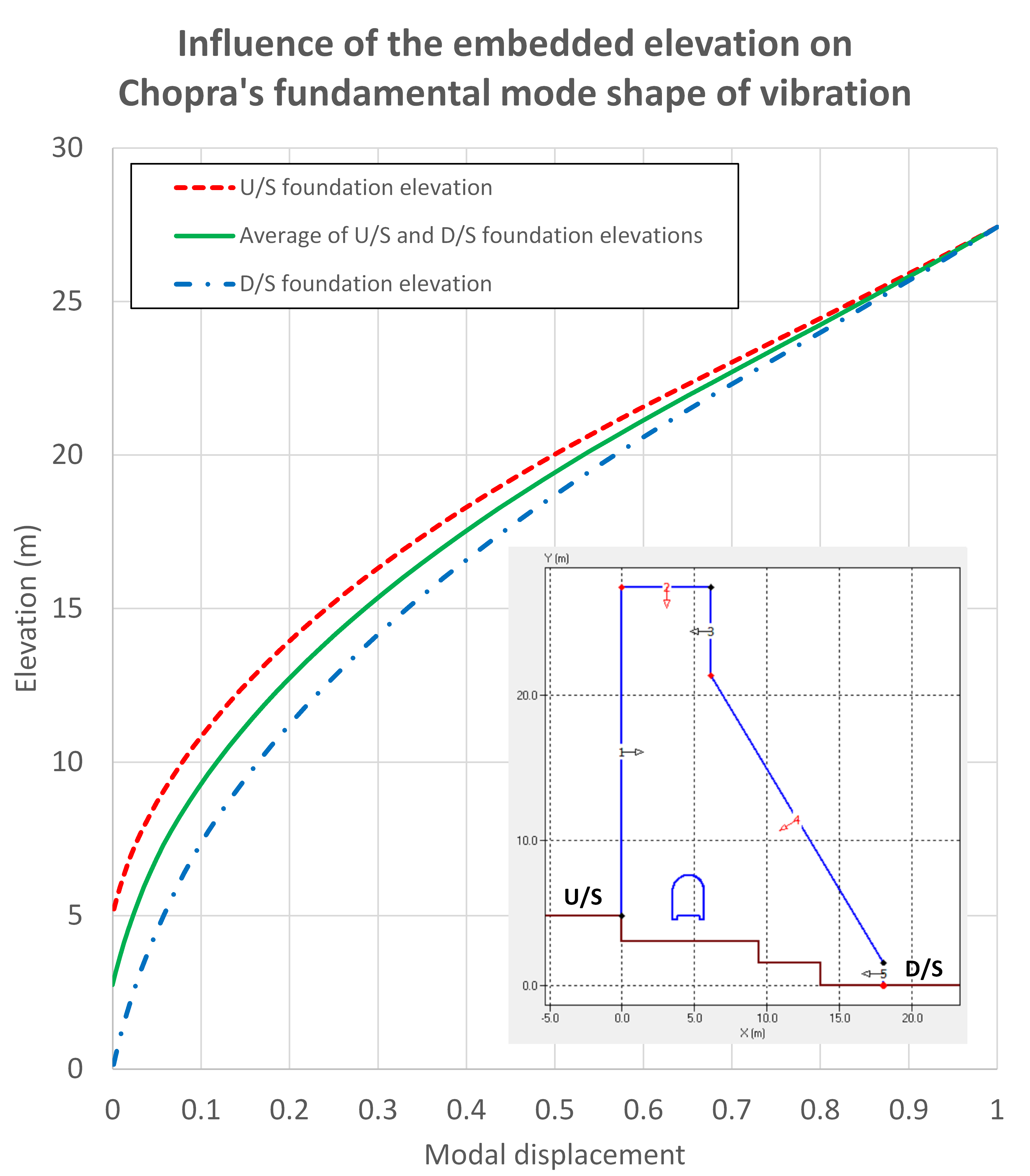
Figure 152
Figure 152 illustrate the influence of the embedded elevation on Chopra’s fundamental mode shape of vibration for a 27m high gravity dam with an inclined foundation profile using the Finite Element Method to compute the first mode of vibration. The embedded elevation will affect the natural period of vibration, spectral accelerations, the fundamental mode shape of vibration, inertia loads (both first and higher modes) and hydrodynamic loads (both first and higher modes). This elevation should be selected with caution as shown in the table below.

Modal combinations
The maximum response of the fundamental and higher vibration modes of vibration do not occur at the same time. A modal combination must, therefore, be considered. Four options are available (Figure 153):
• Only the first vibration mode;
• Only the higher modes of vibration (static correction);
• SRSS (square root of the sum of the squares of the first and higher modes);
• Absolute sum of modes that yields conservative results.
SRSS is often considered the most appropriate option.
Figure 153